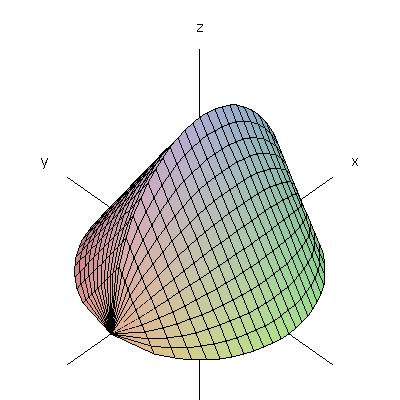
Here is the solid discussed in class on Tuesday.

The base of the solid is the unit circle x²+y²=1, and the cross-section at x is an equilateral triangle (as shown in the figure below).

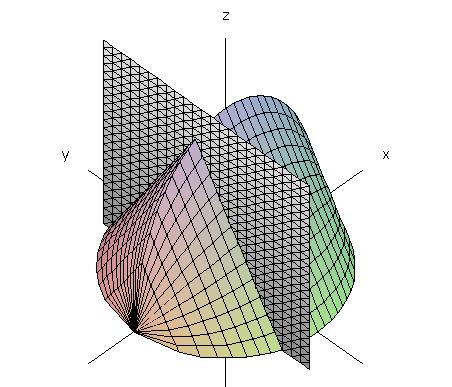
As one student suggested in class, the cross-sections parallel to the base (that is, parallel to the xy-plane) look sort of like "footballs".

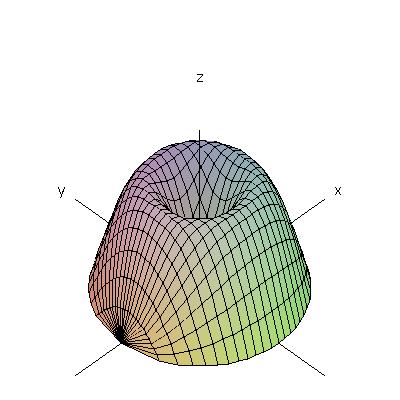
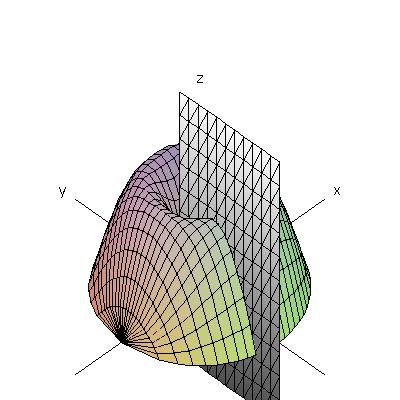
The following figure shows the "bundt cake" discussed in class on Wednesday. This is the solid obtained by rotating about the y-axis the area under the graph of y=sin x, between x=0 and x=π.

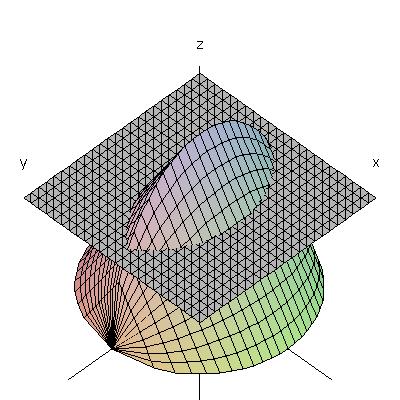
This figure shows a cross-section perpendicular to the x-axis; you can see that the plane meets the solid in a sine curve.

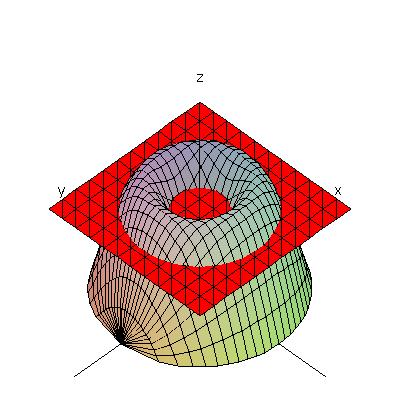
This figure shows a cross-section parallel to the xy-plane. I've drawn the plane in red this time to make the cross-section more easily visible; you can see that it is an annulus.

These pictures were produced using the software package Maple.